C++ 'ın ondalık sayılardaki davranışını, pardon garip davranışını inceliyoruz. Biraz bildiğiniz ve anlamlandırabileceğiniz aritmetiğin dışına çıkmış olacağız. Bakalım neler var; bir for döngümüz olsun, 0 dan başlasın ve 2 ye eşit olmadığı sürece dönmeye devam etsin, adımlarımızda 0.01f olsun, beklentimiz ne olurdu bu durumda 0, 0.01, 0.02 ... şeklinde devam ederek 1.98, 1.99 ve son olarak 2.0 olur ve döngümüz sonlanır diye hayal ediyoruz, ancak beklenmedik şekilde döngümüz asla sonlanmıyor 😱
kodumuz şöyle isteyen deneyebilir :
float total = 0; for (float a = 0; a != 2; a += 0.01f) { total += a; }
net bir ifade olan a != 2 dediğimiz yeri biraz daha yumuşatalım ve a < 2; yapalım, bu durumda a 2 den illaki büyük olacak ve döngü sonlanacak, sonlanacak sonlanmasına da burda da bir sürpriz bekliyor bizi, total değişkeni 199 değil 201 olacak, bu olan bilgisayarlar işlemciler için IEEE754-Compliant standard yayınlamıştır. Bunun olmasının sebebi ondalıklı sayıların değerlendirildikleri değerlere yakın bir sayıyla temsil edilebiliyor olmalarıdır şöyle bir görsel paylaşayım da netleşsin mevzu:
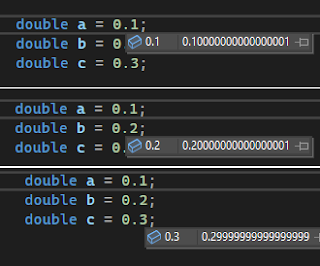
0.1, 0.2 ve 0.3 için aslında yapılan değerlendirmeler şekildeki gibi oluyor, haydi test edelim mi
double a = 0.1; double b = 0.2; double c = 0.3; if (a + b == c) //This never prints on IEEE754-compliant machines std::cout << "This Computer is Magic!" << std::endl; else std::cout << "This Computer is pretty normal, all things considered." << std::endl;
matematiksek olarak c = a + b doğru olmalı ama malesef değil, bu durumu float double kullanırken mutlaka göz önünde bulundurun demiş olayım.
Olayın sebebine bakalım mı? Bizler insan evlatları olarak 10 luk sayı sistemini kullanır ve ondan anlarız, ancak işlemciler/mikrodenetleyiciler elektronik sistemler olmaları sebebiyle ancak voltaj kontrolü yapabilirler ve voltaj bulurlarsa bunu 1, bulamazlarsa 0 olarak değerlendirirler, yani anladıkları tek sayısal sistem binary system 'dir. 0.1, 0.2 gibi sayılar 10'a bölme gerektirdiğinden, (1/10 yapılarak elde edilmiştir) ve bölümün kusursuz olması (yani sonsuza gitmemesi) gerektiğinden, ikili sistemde ifade edilmesi imkansızdır, sayı bu değere asla ulaşamaz ancak çok yaklaşabilir. Eğer ki 0.5 den bahsediyor olsaydık bu mümkündü : binary sistemde noktadan sonraki ilk hane 0.1 -> 1/2 ile çarpılıyor bu da bize tam olarak 0.5 değerini verir, bir sonraki basamak 1/4 ile çarpılıyor, bu durumda 0.25 sayısı da binary sistemde kusursuz olarak ifade edilebilir -> 0.01 ya da her ikisinin toplamı olan 0.75 sayısı 0.11 ile tam ve kusursuz ifade edilebilir. Basamaklar sağa doğru ilerledikçe hep 1 bölü 2 üzeri bir rakam şeklinde dolayısıyla 2 nin üs katları şeklinde ilerliyor ve her ne şekilde olursa olsun oluşan sayının içerisinde 5 olamayacağından (5 nerden geldi? 10 'un çarpanlarından, 10 = 2*5) dolayı bir imkansızlık söz konusu. Ee 0.5 de 5/10 değil mi orda da 5 var? var mı gerçekten ? 5/(5*2). Bizim de onluk sistemde 1/3 için yaşadığımız kusursuz olamama probleminin binary sistemdeki karşılığından bahsediyorum: 0.33333333 elde ettikten sonra, sonsuza doğru giden 3 'ler yerine, hata payının kabul edilebilir olduğu bir yerde durup, hayatımıza kaldığımız yerden devam ediyor olmamıza benzetebiliriz bu durumu. Sözü geçen kabul edilebilir de olsa hata payı ifadesi sayıyı tam olarak kusurlu/hatalı İngilizce deyimle imperfect hale sokuyor. Double için konuşuyorsak noktadan sonra 23 haneye kadar tutması mümkün olduğundan hata payı çoğu zaman çok çok kabul edilebilir olacaktır. Çok takılmayın ama aklınızda kalsın float varsa bölme vardır bölme varsa sıkıntı vardır :) deyip mevzu kontrolden çıkmadan ufak ufak uzaklaşayım.
bu arkadaşların hafızada nasıl saklandıklarına bakalım son olarak :
double a = 0.1 : 0011111110111001100110011001100110011001100110011001100110011010
double b = 0.2 : 0011111111001001100110011001100110011001100110011001100110011010
double c = 0.3 : 0011111111010011001100110011001100110011001100110011001100110011
iken;
a + b : 0011111111010011001100110011001100110011001100110011001100110100
şeklinde yer buluyor hafızada, hocam bunlara nasıl ulaştınız? tarif edeyim : if satırına bir adet breakpoint yerleştirip kodumuzu çalıştırıyoruz, program breakpoint te durduğu zaman, Visual Studio 2022 için konuşuyorsak : Debug->Windows->Memory-> Memory 1 ya da Ctrl + Alt + M, 1 kısa yolu ile hafıza penceremize ulaşıyoruz Address: yazan yere &a yazıp enter a basıyoruz :
double kardeşimiz 8bytes; çıkan ilk 8 haneyi (her hane bir byte ifade eder) kopyalıyoruz : 9a 99 99 99 99 99 b9 3f buradan elde ettiğimiz sayı hex formatında olmanın yanında little-endian da formatında yani ikişerli grupları yer değiştirip en sonrakini en başa alacak şekilde yer değiştirerek aslında ifade edilen sayıyı elde ediyoruz, bu c++ nin veriyi hafızada saklama rutiniyle alakalı bir durum. Değişimden sonra elimizde olan : 3fb999999999999a bunu da windows calc ile programmer modundayken HEX seçili vaziyette yazarsan, binary halini görüyor olacaksın ona da bir görsel bırakalım :
Önceki konu : C++ Aritmetik Operatörler ve öncelikleri
Sonraki konu : C++ Dersleri | Bit İşlemleri - Bitwise Operators
Video :













Hiç yorum yok:
Yorum Gönder